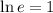The general exponential form can be converted to logarithm form as follows
where ln denotes the natural logarithm. In our case, a is equal to 1 and b is the number e, so we get
Therefore, the answer is
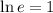
Second way.
We hace the following equation:
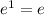
By applying natural logarithm in both sides, we have
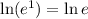
But
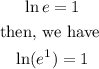
By the logarithm property:
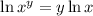
we have that
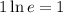
since every number times 1 is the same number,(that is, 1 times lne is lne), we get