we have the function
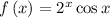
Find out the critical points
so
Find out the first derivative
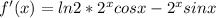
Equate the first derivative to zero
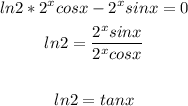
the value of the tangent is positive
that means
the angle x lies on the I quadrant or III quadrant
but remember that the interval is [0, pi]
therefore
The angle x lies on the quadrant
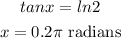
The critical point is x=0.2pi radians
Find out the second derivative
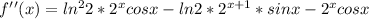
Evaluate the second derivative at x=0.2pi radians
The value of the second derivative is negative
so
The concavity is down
that means
The critical point is a local maximum in the given interval