Answer:
See below.
Explanation:
Hi there!
We want to find the equation of the line that has a slope (m) of 1 and that passes through the point (-10, -6)
There are 3 ways to write the equation of the line:
- Slope-intercept form, which is y=mx+b, where m is the slope and b is the y intercept
- Point-slope form, which is
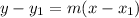 , where m is the slope and
, where m is the slope and
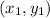 is a point
is a point - Standard form, which is ax+by=c, where a, b, and c are free integer coefficients, but a and b cannot be equal to zero, and a cannot be negative
Since we are given both a point and a slope in this situation, it makes sense to write the equation in point-slope form.
Let's label the values of everything we were given to avoid confusion and mistakes:
m=1
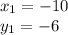
Now substitute these values into the equation (note: we have NEGATIVE numbers, while the formula gives SUBTRACTION, which is why we're subtracting a negative)
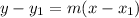
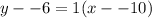
Simplify:
y+6=1(x+10)
The equation can be left as this, or it can be converted into slope-intercept form if you wish.
In that case, we would distribute 1 to each number on the right side.
y+6=x+10
Then, we'll isolate y on one side. Subtract 6 from both sides.
y=x+4
You can also convert it into standard form if you would prefer it that way. To do that, start with slope-intercept form, which we earlier found as y=x+4
In standard form, x and y are on the same side. So subtract x from both sides to move it
-x+y=4
Remember we don't want a (the coefficient in front of x) to be negative. In order to flip the sign, multiply both sides by -1
x-y=-4
Therefore, the answer can be written as y+6=1(x+10), y=x+4, or x-y=4.
Hope this helps!