Given:
In 1960, the population of a town was 13000 people.
Over the course of the next 50 years, the town grew at a rate of 30 people per year.
let t=0 be 1960, and t=1 be 1961
So, the population will increase by a constant number each year.
The equation to find the population will be as follows:
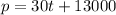
A) Assuming this continues, what is the population predicted to be in `2040`?
So, t = 2040 - 1960 = 80
Substitute t = 180
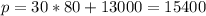
=================================================================
B) Set up and solve the equation to find in which year the population will reach `16` thousand
Now, we will find the number of years the population will reach 16000
So, substitute p = 16000 then solve for (t)
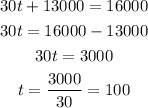
So, the year will be = 1960 + 100 = 2060
================================================================
So, the answer will be:
(A) = 15400 people
(B) 2060