Question

Find the missing parts of the triangle. Round to the nearest tenth when necessary or to the nearest minute as appropriate.a = 8.6 in.b = 13.9 in.c = 16.5 in.

Answer 1

The theorem of cosine can be written in order to find the angles of the triangle when the three sides of the triangle are given but none of the angles,

`\begin{gathered} \cos A=(b^2+c^2-a^2)/(2bc) \\ \cos B=(a^2+c^2-b^2)/(2ac) \\ \cos C=(a^2+b^2-c^2)/(2ab) \end{gathered}`

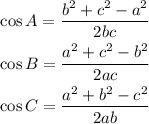
then, apply the theorem at least to find 2 angles. and solve using the arccosine.

For A:

`\begin{gathered} \cos A=((13.9)^2+(16.5)^2-(8.6)^2)/(2\cdot13.9\cdot16.5) \\ \cos A=(391.5)/(458.7) \\ A=\cos ^(-1)((391.5)/(458.7)) \\ A\cong31.4 \end{gathered}`

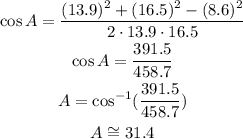
for B:

`\begin{gathered} \cos B=((8.6)^2+(16.5)^2-(13.9)^2)/(2\cdot8.6\cdot16.5) \\ \cos B=(153)/(283.8) \\ B=\cos ^(-1)((153)/(283.8)) \\ B=57.4 \end{gathered}`

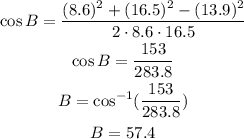
Then, since the sum of all interior angles of any triangles must be 180°, find the missing angles:

`\begin{gathered} A+B+C=180 \\ 31.4+57.4+C=180 \\ C=180-31.4-57.4 \\ C=91.2 \end{gathered}`

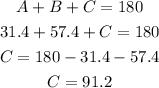
Answer:

The corresponding angles for the measurement of the sides given are A=31.4°, B=57.4° and, C=91.2°.