Answer:
As the values of the domain increase, the values of the function also increase.
Step-by-step explanation:
Given the below function;
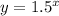
Let's go ahead and evaluate the above function over the domain {-1, 0, 1, 2} as shown below;
When x = -1;
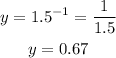
When x = 0;
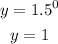
When x = 1;
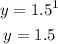
When x = 2;
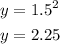
We can see that as the values of the domain increase, the values of the function also increases.