Question

The radius of a Hillstone varies directly with amount of time that it was in a club after a Hillstone has been in particular cloud for 10 seconds it’s radius was 0.5 inches how long would it have to be in the cloud to have a radius of 1.25 inches

Answer 1

Let the radius be r and the time be t.

As per condition, r is proportional to t.

`r=kt`

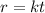
Now it is given that for r=0.5, t=10, so it follows:

`\begin{gathered} 0.5=k(10) \\ k=0.05 \end{gathered}`

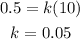
So the equation becomes:

`r=0.05t`

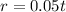
Here r is in inches and t is in seconds.

For r=1.25, the value of t is:

`\begin{gathered} 1.25=0.05t \\ t=(1.25)/(0.05) \\ t=25 \end{gathered}`

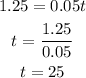
So the value of t is 25 seconds.