According to the graph, angles 7 and 3 are corresponding angles, which means they are equal.
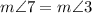
Replacing the given expressions, we have
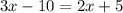
Now, we solve for x
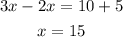
Then, we use this value to find angle 7.
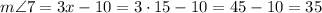
The diagram shows that angle 7 is equal to angle 1 because they are alternate exterior angles.
Hence, angle 1 measures 35°. The right answer is C.