Question

The position of a particle as it moves along the x axis is given for t > 0 by x = (t 3 - 3t 2 + 6t) m, where t is in s. Where is the particle when it achieves its minimum speed (after t = 0)?

Answer 1

Given

t>0

`x=t^3-3t^2+6t`

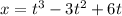
Procedure

Speed would be:

`v=3t^2-6t+6`

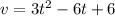
This is the graph for the particle velocity. As you can see the graph corresponds to a parabola that has its minimum value when the time t is equal to 1.

The x-axis corresponds to the time and the y-axis corresponds to the velocity.

Now, with that minimum velocity-time, we can calculate the position using the initial equation that describes the particle position for each time.

`\begin{gathered} t=1 \\ x=1^3-3\cdot1^2+6\cdot1 \\ x=1-3+6 \\ x=4 \end{gathered}`

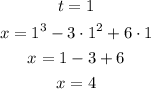
The particle will be in position 4