Question

A car approaches the top of a hill that is shaped like a vertical circle with a radius of 49.9 m. What is the fastest speed that the car can go over the hill without losing contact with the ground?

Answer 1

22.11 m/s

Step-by-step explanation:

The force acting on the car are its weight and the normal force. Then,

`\begin{gathered} \text{F}_{\text{net}}=mg-N=ma_c \\ mg-N=m(v^2)/(r) \end{gathered}`

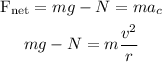
Since it is a circular path the net force is equal to mass times the centripetal acceleration, so we get the equation above.

When the car loses contact with the ground, the normal force is 0, so the given equation is

`mg=m(v^2)/(r)`

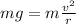
Then, we can solve for v as follows

`\begin{gathered} g=(v^2)/(r) \\ gr=v^2 \\ v=\sqrt[]{gr} \end{gathered}`

Therefore, replacing g = 9.8 m/s² and r = 49.9 m, we get

`v=\sqrt[]{(9.8)(49.9)}=22.11\text{ m/s}`

So, the fastest speed that the car can go over the hill without losing contact with the ground is 22.11 m/s