Question

Write a system of equations to describe the situation below, solve using substitution, and fill in the blanks.Two groups of workers are painting a bridge in the bay. The first group is responsible for painting the north side of the bridge, and the second group is responsible for painting the south side of the bridge. The first group has already painted 3 kilometers of the bridge and is painting 3 additional kilometers per day. The second group has already painted 5 kilometers of the bridge and is painting 1 additional kilometer per day. After a while, the two groups will have painted the same amount of the bridge. How much of the bridge will each group have painted? How long will that take?

Answer 1

Let x be the number of days each group has painted and let y be the number of km each has painted.

We know that the first group already painted 3 km and that each day the paint 3 km, this means that the total km they have painted is:

`y=3x+3`

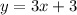
We also knoe that the second group already painted 5 km and that the paint 1 km each day, then the total can be express as:

`y=x+5`

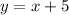
Hence we have the system of equations:

`\begin{gathered} y=3x+3 \\ y=x+5 \end{gathered}`

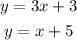
To solve it we substitute the value of y of the first equation into the second equation, then we have:

`\begin{gathered} 3x+3=x+5 \\ 3x-x=5-3 \\ 2x=2 \\ x=(2)/(2) \\ x=1 \end{gathered}`

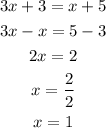
Plugging the value of x in the first equation we have that:

`\begin{gathered} y=3(1)+3 \\ y=3+3 \\ y=6 \end{gathered}`

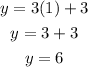
Therefore:

Each group have painted 6 km.

It takes one day for the groups to pain the same amount.