According to the given data we have the following expression:
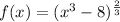
To find f'(x) we would have to make the following calculation:
First:
Apply the chain rule
So:
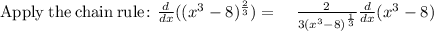
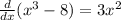
So:
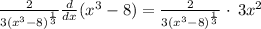
Next, you would have to simplify the expression above:
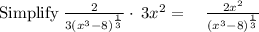
Therefore:
![\frac{2x^2}{\left(x^3-8\right)^{(1)/(3)}}=\frac{2x^2}{\sqrt[3]{x^3}^{}-8}](https://img.qammunity.org/2023/formulas/mathematics/college/a2ox5v6z4c7eufxnrnwqpoacrogzs22d1r.png)
Therefore, the right answer is
![f^(\prime)(x)=\frac{2x^2}{\sqrt[3]{x^3}^{}-8}](https://img.qammunity.org/2023/formulas/mathematics/college/j818h05gm21cnkqjh2rttrqeyxr2vnvdoe.png)