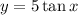Question

The function graphed to the right is of the form y=a tan bx or y=a cot bx for some a ≠ 0, b > 0. Determine the equation of the function. (Half- and quarter-points are identified by dots.)

Answer 1

We are given the graph of a function of the form:

`y=a\tan (bx)`

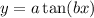
To determine the values of "a" and "b" we will first use the fact that the asymptotes of the graph are the points where the value of the angle of the tangent is 90 degrees. Therefore, if the first asymptote is at:

`bx=(\pi)/(2)`

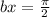
And we know from the graph that the value of "x" is:

`x=(\pi)/(2)`

The substituting we get:

`b((\pi)/(2))=(\pi)/(2)`

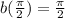
Simplifying we get:

`b=1`

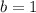
Substituting we get:

`y=a\tan (x)`

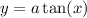
Now, to determine the value of "a" we will use the following point in the graph:

`(x,y)=((\pi)/(4),5)`

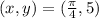
Substituting we get:

`5=a\tan ((\pi)/(4))`

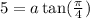
We have that:

`\tan ((\pi)/(4))=1`

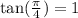
Substituting:

`5=a`

Therefore, the value of "a" is 5. The function is:

`y=5\tan x`