Solve for the slope and equation for each of the function B(x), G(x) and T(x)
Solving for B(x)
We have the following points for B(x)
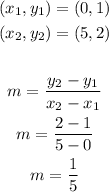
Use the point (0,1) to solve for the equation of B(x)
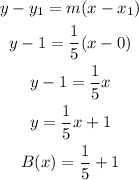
Solving for G(x)
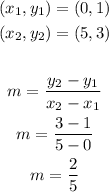
Use the point (0,1) to solve for the equation G(x)
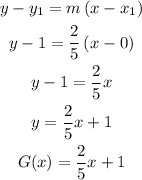
Solving for T(x)
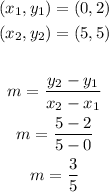
Use the point (0,2) to solve for the equation T(x)
Substituting x = 4 to B(x), G(x), and T(x)
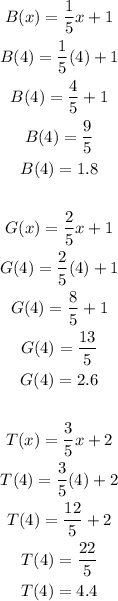
Therefore, B(4) = 1.8, G(4) = 2.6, and T(4) =4.4