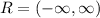Question

Y=inxCan you please give a graph use color for function, asymptotes, etc.A short table of easy pointsThe domain and rangePlease identify and label the asymptotes (Please work this as if you didn’t have a calculator)

Answer 1

To graph the natural logarithm function, without using a calculator, and using a short table of easy points, we can proceed as follows:

1. We need to remember that the logarithm function is not defined for negative numbers. We cannot find any exponent that raised to a positive number that result in a negative number.

2. The logarithm function is not defined for x = 0. Therefore, we will have an asymptote at x = 0. It is a vertical asymptote, x = 0.

3. The value for ln(1) = 0, and we also know that the value of ln(e) = 1.

We need to remember that e is, approximately, 2.7182818284...

Now, using this information, we will have the following table:

x - values ---------- y-values

Negative values ---- the function is not defined

0 ------------- The function has a vertical asymptote

1 ------------- 0

e (approx. 2.72) ------------ 1

We can see the table of these values in the following drawing:

Now we can sketch a graph of this function as follows:

The domain of the natural logarithm function is, in interval notation:

`D=(0,\infty)`

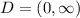
And the range is (in interval notation too) as follows:

`R=(-\infty,\infty)`