Question

Express z1 33 - 9i in polar form.Express your answer in exact terms, using radians, where your angle is between 0 and 21 radians, inclusive.21 =

Answer 1

`z_1=6\sqrt[]{3}\lbrack\cos (-(\pi)/(3))+i\sin (-(\pi)/(3))\rbrack`

Step-by-step explanation:

The rectangular form of a complex number is generally given as;

`z=a+bi`

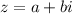
where;

`\begin{gathered} a=r\cos \theta \\ b=r\sin \theta \\ r=|z|=\sqrt[]{a^2+b^2} \\ \theta=\tan ^(-1)((b)/(a))\text{ for a > 0} \end{gathered}`

Converting rectangular form to polar form, we'll have;

`z=r(\cos \theta+i\sin \theta)`

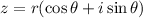
Given the below;

`z_1=3\sqrt[]{3}-9i`

We can see that;

`\begin{gathered} a=3\sqrt[]{3} \\ b=-9 \end{gathered}`

Let's go ahead and find r as shown below;

`\begin{gathered} r=\sqrt[]{(3\sqrt[]{3})^2+(-9)^2}=\sqrt[]{(9*3)^{}+81}=\sqrt[]{27+81}=\sqrt[]{108} \\ r=\sqrt[]{36*3}=\sqrt[]{36}*\sqrt[]{3} \\ r=6\sqrt[]{3} \end{gathered}`

Let's now find theta,;

`\begin{gathered} \theta=\tan ^(-1)(\frac{-9}{3\sqrt[]{3}})=-(\pi)/(3) \\ \\ \end{gathered}`

If we go ahead and input the above values into our polar form equation, we'll have;

`z_1=6\sqrt[]{3}\lbrack\cos (-(\pi)/(3))+i\sin (-(\pi)/(3))\rbrack`