Answer:
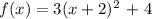
Step-by-step explanation:
The general form of a quadratic equation in the vertex form is:

where the vertex would be (h,k)
Thus, we have the equation as:
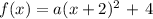
The value of a will determine how narrow the function would look when plotted
Mathematically, we have the parent function as when a = 1
The higher the value of a, the narrower the plot would look
Putting this into consideration, we have the equation as:
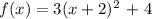
Kindly note that if a is 4, we would have a narrower plot than the parent function where a is adjudged to be equal to 1
However, if a is 1/3 (a positive number less than 1), we would have a broader plot