The given equations are
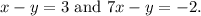
The given point is (-1,-4)
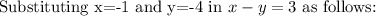
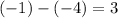

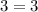
This equation is true.
When (-1,-4), substituted into the first equation, the equation is true.
The second option is correct.
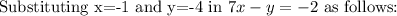
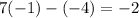

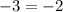
This equation is not true.
When (-1,-4), substituted into the second equation, the equation is false.
The third option is correct.
If the ordered pair (-1,-4) is a solution to the system of linear equations, it should satisfy both linear equations.
When (-1,-4), substituted into the second equation, It does not satisfy this equation.
Hence the ordered pair (-1,-4) is not a solution to the system of linear equations.
Correct options are two, three and six.