Question

Question 22 0147 How many times does the quadratic function below intersect the x-axis? y-2x +7x+6

Answer 1

Hello there. To solve this question, we'll have to remember some properties about functions.

We want to determine how many times does the graph of the following quadratic function intersects the x-axis:

`y=2x^2+7x+6`

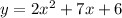
For this, we'll have to find how many roots does it have, by plugging in y = 0:

`2x^2+7x+6=0`

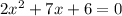
Remember for a quadratic equation as:

`ax^2+bx+c=0,a\\eq0`

The solution for x is given by:

`x=(-b\pm√(b^2-4ac))/(2a)`

But in this case, we don't really need to determine the roots and only see how many of them the function have.

In this case, we evaluate the expression inside the square root, also called the discriminant of the equation.

`\Delta=b^2-4ac`

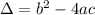
If Δ is greater than zero, the function haves 2 distinct real roots.

If Δ is equal to zero, the function have 2 equal real roots (or 1 real root)

If Δ is less than zero, the function does not have real roots (two conjugate complex roots)

Plugging in the values of a = 2, b = 7 and c = 6, we have:

`\Delta=7^2-4\cdot2\cdot6=49-48=1`

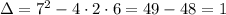
This means that this function intersects the x-axis two times.

The answer to this question is: 2.