Given:
The angle is 240 degrees.
Required:
We need to find the six trigonometric functions.
Step-by-step explanation:
Consider the sine function.
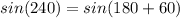
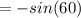
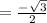
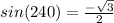
Consider the cosine function.
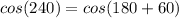
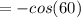
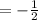
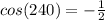
Consider the tan function.
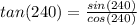
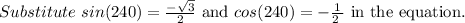
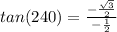
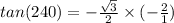
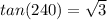
Consider the cot function.
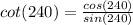
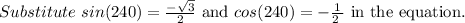
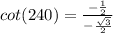
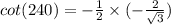
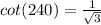
Consider the sec function.
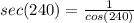
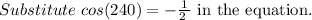
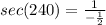
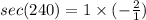
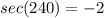
Consider the csc function.
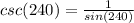
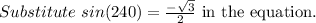
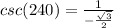
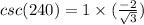
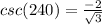
Consider the angle in a graph:
Final answer:
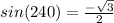
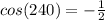
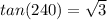
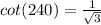
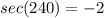
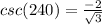
The angle lies in the third quadrant.