Question

Finding angle measures of a right ofIn A ABC with right angle B, suppose that m ZA= (5x+6)° and m ZC = (4x-6).Find the degree measure of each angle in the triangle.(5x + 6)BAm A =xm ZB =口。m 2C =+(4x - 6).

Answer 1

We have the following situation:

We need to find the degree measure of each angle, A, and C since we already know that angle B = 90 degrees.

To answer this question, we need to remember that the sum of the interior angles of a triangle is equal to 180 degrees.

Then we can write the next equation to find the value of x as follows:

`\begin{gathered} m\angle A=(5x+6)^(\circ) \\ m\angle C=(4x-6)^(\circ) \end{gathered}`

`(5x+6)^(\circ)+(4x-6)^(\circ)+90^(\circ)=180^(\circ)`

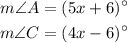
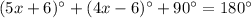
Now, we need to add the like terms as follows:

`\begin{gathered} (5x+4x+6-6+90)^(\circ)=180^(\circ) \\ (9x+90)^(\circ)=180^(\circ) \end{gathered}`

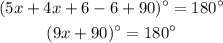
Now, we can subtract 90 from both sides of the equation:

`\begin{gathered} (9x+90-90)^(\circ)=(180-90)^(\circ) \\ (9x)^(\circ)=90^(\circ) \end{gathered}`

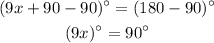
If we divide both sides by 9, we finally have for x:

`\begin{gathered} (9x)/(9)=(90)/(9) \\ x=10 \end{gathered}`

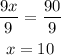
Therefore, the value for x = 10.

If we substitute the value of x into the corresponding expressions for angles A and C, then we have:

Finding the measure of angle A

`\begin{gathered} x=10^{}\Rightarrow m\angle A=(5x+6)^(\circ) \\ m\angle A=(5(10)+6)^(\circ)=(50+6)^(\circ)=56^(\circ) \\ m\angle A=56^(\circ) \end{gathered}`

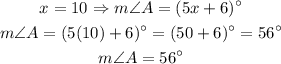
Finding the measure of angle C

We can proceed in a similar way here. Then we have:

`\begin{gathered} x=10^{}\Rightarrow m\angle C=(4x-6)^(\circ) \\ m\angle C=(4(10)-6)^(\circ)=(40-6)^(\circ)=34^(\circ) \\ m\angle C=34^(\circ) \end{gathered}`

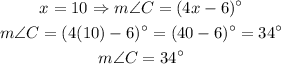
Therefore, in summary, we can say that:

`\begin{gathered} m\angle A=56^(\circ) \\ m\angle B=90^(\circ) \\ m\angle C=34^(\circ) \end{gathered}`

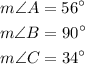
[We already knew that the measure of angle B is 90 degrees (right angle).

We can also check that the sum of all the angles is equal to 180 degrees:

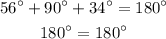
`\begin{gathered} 56^(\circ)+90^(\circ)+34^(\circ)=180^(\circ) \\ 180^(\circ)=180^(\circ) \\ \end{gathered}`

.]