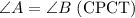Given data :
AD=BC
BC is perpendicular to AE
AD is perprndicular to BE
In the given Figure,
BC is perpendicular to AE so, angle BCE =90 degree
Similarly, AD is perprndicular to BE so, angle ADE = 90 degree
And in the triangle ADE and BCE,
angle E is common in both triangles
Since, AD=BC given
So,

From the property of congurency,(CPCT) all the corresponding sides and angles of congurent triangles are equal so,