Given:

Required:
Probability of removal of the crayon as blue, red, and yellow respectively
Step-by-step explanation:
The probability of removal of the first blue crayon is calculated as,

The probability of removal of the second red crayon is calculated as,
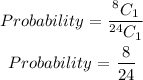
The probability of removal of the third yellow crayon is calculated as,
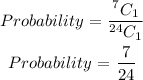
Therefore the required probability is calculated as,
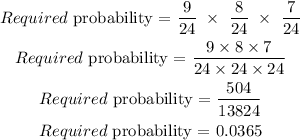
Answer:
Thus the required probability is 0.0365