ANSWER
x = 0°, 180°, 210°, 330°
Step-by-step explanation
We have to find x when both functions have the same value,
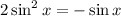
Add sin(x) to both sides,
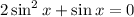
And we have a quadratic equation, where the variable is sin(x). Factor out 2 sin(x),
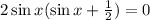
The solutions are,
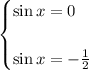
Now we have to find the values of x whose sine is 0 and the ones whose sine is -1/2,
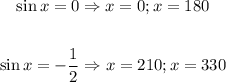
Hence, the values where they are the same are 0°, 180°, 210° and 330°