Given:
Purchased Value = $29,500
Value decreased by 20%
Time = 5 year
Find-: Value after 5 years.
Sol:
Value decreased by 20% that mean:
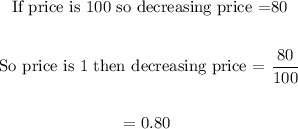
Unit price decreased by 0.80 so decreasing price after one year is:
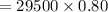
Decreasing price after 2 year is:
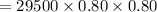
So decreasing value after "t" year is:
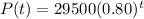
Decreasing value after 5 year is:
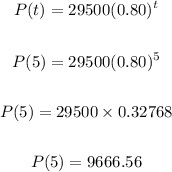
So the price is after 5 years 9666.56