Question

Which standard form of the equation of the hyperbola has vertices at? Thank you!

Answer 1

x²/25 - y²/144 = 1

Step-by-step explanation:

In a hyperbola with an equation

`(x^2)/(a^2)-(y^2)/(b^2)=1`

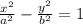
The vertices are (a, 0) and (-a, 0) and the asymptotes are y = ±(b/a)x

In this case, the vertices are (5, 0) and (-5, 0), so the value of a is 5.

And the asymptote is y = ±(12/5)x, so the value of b is 12.

Then, replacing a = 5 and b = 12, we get that the equation of the hyperbola is

`\begin{gathered} (x^2)/(5^2)-(y^2)/(12^2)=1 \\ \\ (x^2)/(25)-(y^2)/(144)=1 \end{gathered}`

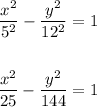
Therefore, the answer is

x²/25 - y²/144 = 1