Question

Find the value of the variable. Round to the nearest whole number.N8760PX≈y≈yo63toR

Answer 1

TO FIND X

We can use the Cosine Trig Ratio to evaluate the value of x given to be:

`\cos\theta=(adj)/(hyp)`

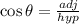
From the triangle, we have the following parameters:

`\begin{gathered} \theta=x \\ adj=PR=63 \\ hyp=NR=87 \end{gathered}`

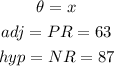
Therefore, the angle can be calculated as follows:

`\begin{gathered} \cos x=(63)/(87) \\ x=\arccos((63)/(87)) \\ x=43.6\degree \end{gathered}`

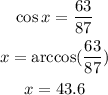
To the nearest whole number, the value of x is 44 degrees.

TO FIND Y

The value of y can be calculated using the sum of angles in a triangle, give =n to 180 degrees.

Therefore, the missing angle can be calculated to be:

`\begin{gathered} 90+x+y=180 \\ 90+44+y=180 \\ y=180-44-90 \\ y=46\degree \end{gathered}`

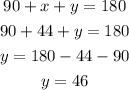
The value of y is 46 degrees.