Question

Let p be "n is greater than 2 and even" and q be "n is not prime." Represent the statement "If n is greater than 2 and even, then n is not a prime" in symbolic form.Select the correct answer below:∼p⟹∼qp⟹qp⟹∼q∼p⟹q

Answer 1

option (b)
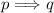`$p \Longrightarrow q$` is the correct option.

Given:

p: n is greater than 2 and even.

q: n is not prime.

The statement is: "If n is greater than 2 and even, then n is not a prime."

This statement implies that if n satisfies the condition of being greater than 2 and even (p), it leads to the conclusion that n is not prime (q).

Therfore, the correct symbolic representation of the statement is indeed
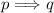`$p \Longrightarrow q$`.

Answer 2

From the question;

We have the statements

`P\text{ = n is greater than 2 and even}`

and

`q=\text{ n is not prime}`

we are to represent in stmbolic form

The statement

`\text{If n is greater than 2 and even, then n is not a prime}`

From this statement

P and q are true statements

hence we can say

`\text{If p then q}`

Therefore

`p\text{ implies q}`

Hence in symbolic form we have

`p\Rightarrow q`