Question

What is the probability of getting a total of 2 in an experiment tossing a pair of dice?

Answer 1

Given:

The objective is to find the probability of getting a total of 2 in tossing a pair of dice.

Since each dice contain 6 sides. So the sample space in rolling two dices is,

`\begin{gathered} \text{n(S)=6}*6 \\ n(S)\text{=3}6 \end{gathered}`

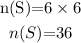
The sample space of getting sum of 2 is,

`\text{Sum of 2=}\lbrace(1,1)\rbrace`

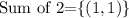
Thus, the number of sample space of getting a sum of 2 is one.

Then, the probability of getting a sum of 2 in rolling a pair of dice is,

`\begin{gathered} P(sum\text{ of 2)=}\frac{n(sum\text{ of 2)}}{n(S)} \\ P(sum\text{ of 2)=}(1)/(36) \\ P(sum\text{ of 2)=}0.0278 \end{gathered}`

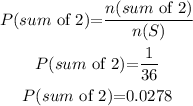
Hence, option (A) is the correct answer.