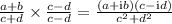Given:
Complex numbers
Step-by-step explanation:
Complex numbers are the numbers that are expressed in the form of,
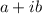
Where, a, and b are real numbers and " i " is an imaginary number.
The value of i is,
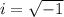
Yes, we can divide the two complex numbers.
If the complex numbers in the division form
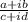
Then multiply and divide by its conjugate to evaluate the division.
Here, the conjugate of the denominator is,
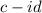
Then, we get