Question

Question 7(Multiple Choice Worth 1 points)(07.02 MC)Factor completely x³ - 2x² - 8x + 16.O(x + 2)(x²+8)O(x-2)(x²+8)O(x + 2)(x²-8)O(x-2)(x²-8)

Answer 1

Given the polynomial:

`x^3-2x^2-8x+16`

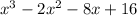
It's required to factor it completely. We need to find the simplest factors that reproduce the given expression.

The first approach is to try to find an integer zero of the polynomial. Testing the value of x = 2 we get:

`\begin{gathered} (2)^3-2(2)^2-8(2)+16 \\ \\ \text{ Operating:} \\ \\ 8-8-16+16=0 \end{gathered}`

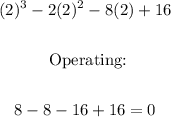
Applying the remainder theorem, the polynomial is divisible by x - 2 because the remainder of the division is 0.

Now we have to find the quotient of:

`(x^3-2x^2-8x+16)/(x-2)`

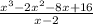
We'll use the synthetic division as follows:

1 -2 -8 16

2 2 0 -16

------------------------

1 0 -8 0

The last row contains the coefficients of the quotient:

`x^2-8`

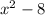
This binomial can be easily factored using the special product formula:

`x^2-a^2=(x-a)(x+a)`

Therefore:

`x^2-8=(x-√(8))(x+√(8))`

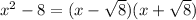
The complete factorization is:

`x^3-2x^2-8x+16=(x-2)(x-√(8))(x+√(8))`

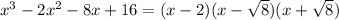
None of the choices corresponds to this result, so we go back to the previous step. Note that this step is not the complete factorization required.

Answer:

`x^3-2x^2-8x+16=(x-2)(x^2-8)`

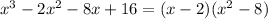
Last choice