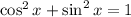Question

What basic trigonometric identity would you use to verify that

Answer 1

Given the equation:

`\frac{\sin^2x+\text{cos}^2x}{\cos x}=\sec x`

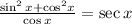
Let's determine the trigonometric identity that you could be used to verify the exquation.

Let's determine the identity:

Apply the trigonometric identity:

`\sin ^2x+\cos ^2x=1`

`\cos x=(1)/(\sec x)`

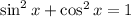
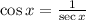
Replace cosx for 1/secx

Thus, we have:

`\begin{gathered} (\sin^2x+\cos^2x)/((1)/(\sec x)) \\ \\ =(\sin ^2x+\cos ^2x)(\sec x) \\ \text{Where:} \\ (\sin ^2x+\cos ^2x)=1 \\ \\ We\text{ have:} \\ (\sin ^2x+\cos ^2x)(\sec x)=1\sec x=\sec x \end{gathered}`

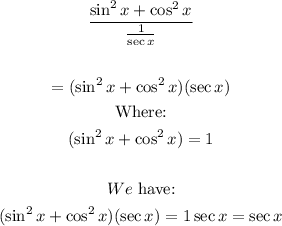
The equation is an identity.

Therefore, the trignonometric identity you would use to verify the equation is:

`\cos ^2x+\sin ^2x=1`

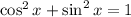
ANSWER:

`\cos ^2x+\sin ^2x=1`