Answer:
500 N/m
Step-by-step explanation:
The potential energy of a spring is equal to
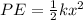
Where k is the spring constant and x is the distance stretched.
Solving the equation for k, we get
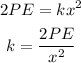
Now, we can replace PE = 10.0 J and x = 0.200 m, so
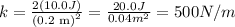
Therefore, the spring constant is 500 N/m