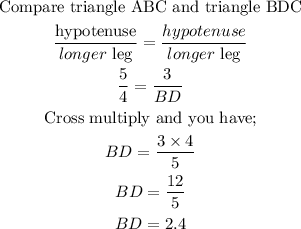Question

Find the lengths of segments AB and BD. Show your answers 2 different ways under show your work.

Answer 1

In the larger triangle, that is triangle ABC, the hypotenuse (longest side) is shown as 5 units (3.2 + 1.8) and one of the other sides is shown as 3. Using Pythagoras' theorem we now have;

`\begin{gathered} AC^2=AB^2+BC^2 \\ 5^2=AB^2+3^2 \\ 25=AB^2+9 \\ \text{Subtract 9 from both sides of the equation} \\ 16=AB^2 \\ \sqrt[]{16}=AB \\ 4=AB \end{gathered}`

In the smaller triangle ABD, the hypotenuse is given as AB. Hence, applying the Pythagoras' theorem as well, we'll now have;

`\begin{gathered} AB^2=AD^2+BD^2 \\ 4^2=3.2^2+BD^2 \\ 16=10.24+BD \\ \text{Subtract 10.24 from both sides of the equation} \\ 5.76=BD^2 \\ \sqrt[]{5.76}=BD \\ BD=2.4 \end{gathered}`

METHOD 2:

We shall look at the bigger and smaller triangles and use their ratios to find the missing sides.

`\begin{gathered} \text{Compare triangle ABC } \\ \text{Hypotenuse}=5 \\ \text{Longer leg=AB} \\ \text{Shorter leg=3} \\ \text{With triangle ABD} \\ \text{Hypotenuse}=AB \\ \text{Longer leg=3.2} \\ \text{Shorter leg=BD} \\ \text{The applicable ratios are;} \\ \text{ABC}\colon ABD \\ \frac{\text{hypotenuse}}{\text{longer leg}}=\frac{hypotenuse}{longer\text{ leg}} \\ (5)/(AB)=(AB)/(3.2) \\ \text{Cross multiply and you have;} \\ 5*3.2=AB* AB \\ 16=AB^2 \\ \sqrt[]{16}=AB \\ 4=AB \end{gathered}`

With AB calculated as 4, we can now solve for BD in triangle ABD using the Pythagoras' theorem (as shown in the earlier solution above).

We can also use the ratios as per the instruction to use a second method and that would be;

`\begin{gathered} \text{Compare triangle ABC and triangle BDC} \\ \frac{\text{hypotenuse}}{longer\text{ leg}}=\frac{hypotenuse}{longer\text{ leg}} \\ (5)/(4)=(3)/(BD) \\ \text{Cross multiply and you have;} \\ BD=(3*4)/(5) \\ BD=(12)/(5) \\ BD=2.4 \end{gathered}`