Question

A salmon-fishing boat put out to sea early in the morning travelling with the tide. It took 20 min to cover the 6 km to the captain's favorite fishing grounds. The return trip was against the tide and took 36 min. What was the still water speed of the boat and what was the speed of the tide?Show work please.

Answer 1

The Speed of the still water: 11.5 km/h

Speed of the tide is 6.5 km/h

1) This is a case of rational equations problem, we need to remind ourselves of that relation evolving speed:

`s=(d)/(t)\Leftrightarrow d=st`

2) Based on that, we can set two equations. One to the salmon swimming with the aid of the tide, and the other against the tide. Note also that we need to convert minutes to hours so that the answer might be km/h

`\begin{gathered} d=st \\ d_1=s_1t \\ 6=(x+y)(20)/(60)=6=(\mleft(x+y\mright))/(3)\Rightarrow(x+y)=18 \\ 6=(x-y)(36)/(60)\Rightarrow6=(x-y)(3)/(5)\Rightarrow3(x-y)=15 \end{gathered}`

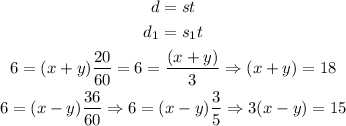
Now we can write out the following system of linear equations in which x is the still water and y is the speed of the tide:

`\begin{gathered} x+y=18 \\ x-y=5 \\ ---------- \\ 2x=23 \\ (2x)/(2)=(23)/(2) \\ x=11.5 \\ \\ x-y=5 \\ 11.5-y=5 \\ y=6.5 \end{gathered}`

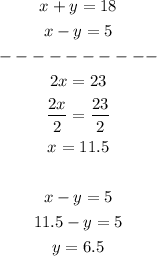
Note that we added both equations simultaneously, eliminating y and then we plugged into that x-y=5,

3) Thus, the answer is the Speed of the still water: 11.5 km/h is the speed of the tide is 6.5 km/h