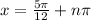Question

Which of the following are solutions to the equation sinx cosx = 1 /4? ? Check all

Answer 1

We are given the following equation:

`sinxcosx=(1)/(4)`

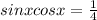
First, we will multiply both sides by 2:

`2sinxcosx=(2)/(4)`

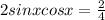
Simplifying the right side:

`2sinxcosx=(1)/(2)`

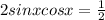
Now, we use the following trigonometric identity:

`2sinxcosx=sin(2x)`

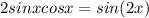
Applying the property we get:

`sin(2x)=(1)/(2)`
`sin(2x)=(1)/(2)`

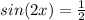
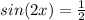
Now, we take the inverse function of sine:

`2x=arcsin((1)/(2))`

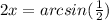
Solving the operation on the right side we have two possible solutions:

`2x=(\pi)/(6)+2n\pi`

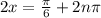
and:

`2x=(5\pi)/(6)+2n\pi`

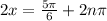
Dividing both sides by 2:

`x=(\pi)/(12)+n\pi`

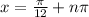
and

`x=(5\pi)/(12)+n\pi`