To determine whether the ordered pair is a solution to the given equation we will follow the process. The equation given to us is as follows:
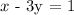
The ordered pair that may or may not satisfiy the above equation is:
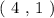
To determine whether the ordered pair staisfies the given equation we will simply plug in the respective values of the ordered pair ( x and y ) into the given equation as follows:
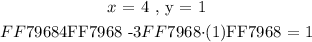
Next we will simplify both sides of the " = " sign and check whether the two sides are numerically equivalent or not:
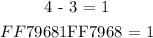
Both sides are equal that means that the ordered pair ( 4 , 1 ) satisfies the given equation and; hence, the ordered pair is a solution!