Question

If angle a=40 degrees and b is 30 cm long, what is the length of c?

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Draw the given triangle

STEP 2: Write the given measures

`\begin{gathered} Using\text{ angle }\alpha \\ \alpha=40\degree,b=adjacent=30,c=hypotenuse \end{gathered}`

STEP 3: State the trigonometric ratio to use

Since we have the adjacent and hypotenuse, we use the tan ratio which is stated below:

`cos\alpha=(adjacent)/(hypotenuse)`

By substitution,

`cos40\degree=(30)/(c)`

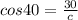
By simplification, we cross multiply

`\begin{gathered} c*\cos40\degree=30 \\ c=(30)/(\cos40\degree) \\ c=39.16221868 \\ c\approx39.16cm \end{gathered}`

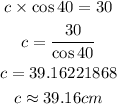
Hence, the length of c is approximately 39.16cm