The height attained by the arrow is modelled as,
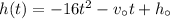
Given that the initial height is 20 ft and the initial velocity is 179 ft per second,
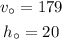
Substitute the values,
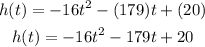
When the arrow hits the ground its height will become zero,
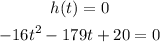
Applying the quadratic formula,
![\begin{gathered} t=\frac{-(-179)\pm\sqrt[]{(-179)^2-4(-16)(20)}}{2(-16)} \\ t=\frac{179\pm\sqrt[]{33321}}{-32} \\ t=(179\pm182.54)/(-32) \\ t=(179+182.54)/(-32),t=(179-182.54)/(-32) \\ t=-11.298,t=0.1106 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/xibaouhjmk8pbvlgm9izfis73zm1e2bz6z.png)
Since time cannot be negative, we have to neglect the negative value.
Thus, it can be concluded that the arrow will hit the ground after 0.1106 seconds approximately.