Question

A park volunteer plans to work on the park's stone walls for 1 hour every Monday, 1 hour every Wednesday, and on Fridays. The graph shows the number of hours he plans to work for a given number of weeks.The constant of proportionality of the line is .The slope of the line is How many hours will the volunteer work in 16 weeks?The volunteer will work in 16 weeks

Answer 1

From the graph we have the following:

Week number Number of hours worked

1 5 hours

2 10 hours

3 15 hours

4 20 hours

Here, the number of hours vary directly with the number of weeks.

To find the constant of proportionality we have:

Where week number is x and number of hours is y, constant of proprtionality = k

y = kx

5 = 1k

`k=(5)/(1)=\text{ 5}`

Constant of proportionality, k = 5

To find the slope, we have:

`\text{slope}=(10-5)/(2-1)=(5)/(1)=5`

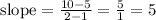
The slope of the line is 5.

To find the number of hours the volunteer will work in 16 weeks we have:

y = 5 x 16

y = 80 hours

The volunteer will work for 80 hours in 16 weeks.

The equation to describe the relationship is:

Use the slope intercept form: y = mx + b

Where m = slope and b = y-intercept

Here y-intercept = 0, and slope = 5

The equation is:

y = 5x + 0

y = 5x

ANSWER:

Constant of proportionality = 5

Slope = 5

The volunteer will work for 80 hours in 16 weeks

Equation: y = 5x