Question

D) The particle displacement due to a sound wave is given by: y = 4.25x10-3 sin[200πt – (2πx /800)]Where x is measured in cm and t in seconds. Write down the amplitude, velocity , wavelength, frequency, andTime period of the wave.Notes:IeI= 1.6 x10-19 C, me=9.1x10-31 kg, mp = 1.67x10-27 Kg, h= 6.62x10-34 J.s, c= 3x108 m/s

Answer 1

Given,

`y=4.25*10^(-3)\sin \lbrack200\pi t-((2\pi x)/(800))\rbrack`

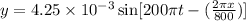
The wave equation of a particle is,

`y=A\sin (\omega t-kx)`

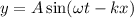
Where

• A is the amplitude.

,

• ω is the angular velocity.

,

• k is the wavenumber.

On comparing the two equations,

Amplitude, A=4.25×10⁻³

Angular velocity, ω=200π rad/s200

The wavenumber, k=2π/800 /m

The velocity of the particle is equal to the time derivative of its displacement.

Thus, the velocity is,

`\begin{gathered} v=(dy)/(dt) \\ =(d)/(dt)(A\sin (\omega t-kx))_{} \\ =A\omega\cos (\omega t-kx) \end{gathered}`

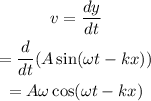
On substituting the known values, the velocity is,

`\begin{gathered} v=4.25*10^(-3)*200\pi*\cos \lbrack200\pi t-((2\pi x)/(800))\rbrack \\ =0.85\pi\cos \lbrack200\pi t-((2\pi x)/(800))\rbrack \end{gathered}`

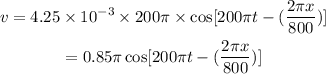
The wavelength is given by,

`\lambda=(2\pi)/(k)`

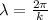
On substituting the known values,

`\begin{gathered} \lambda=(2\pi)/(((2\pi)/(800))) \\ =800\text{ m} \end{gathered}`

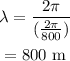
Thus the wavelength is 800 m

The frequency is given by,

`f=(2\pi)/(\omega)`

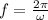
On substituting the known values,

`\begin{gathered} f=(2\pi)/(200\pi) \\ =0.01\text{ Hz} \end{gathered}`

Thus the frequency is 0.01 Hz

The period is given by,

`T=(1)/(f)`

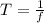
On substituting the known values,

`\begin{gathered} T=(1)/(0.01) \\ =100\text{ s} \end{gathered}`

Thus the time period of the wave is 100 s