Question

Solve the following. List all possible possible solutions for the ambiguous case. #7

Answer 1

The sum of the interior angles of any triangle is always 180º:

`A+B+C=180`

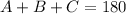
Use the equation above and the given data to find C:

`\begin{gathered} C=180º-A-B \\ C=180º-38º-72º \\ C=70º \end{gathered}`

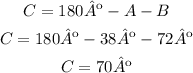
Law of sines:

`(a)/(sinA)=(b)/(sinB)=(c)/(sinC)`

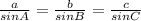
Use the pair of ratios for a and b to solve a:

`\begin{gathered} (a)/(sinA)=(b)/(sinB) \\ \\ a=sinA*(b)/(sinB) \\ \\ a=sin38º*(12)/(sin72º) \\ \\ a=7.8 \end{gathered}`

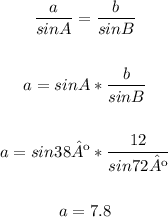
Use the pair of ratios for b and c to solve c:

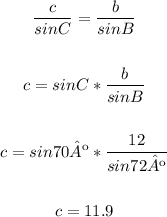
`\begin{gathered} (c)/(sinC)=(b)/(sinB) \\ \\ c=sinC*(b)/(sinB) \\ \\ c=sin70º*(12)/(sin72º) \\ \\ c=11.9 \end{gathered}`Thenm, the solution for the given triangle is:A=38ºB=72ºC=70ºa=7.8b=12c=11.9