Answer:
B. cost = $1.25 x n + $1.25
Step-by-step explanation:
In the store, each item costs exactly $1.25.
Therefore, n items cost $1.25n.
Since you also have to pay $1.25 no matter how many items purchased, the cost function will be:
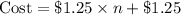
The correct choice is B.