Answer:
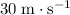 .
.
Step-by-step explanation:
Under the assumptions, the acceleration of this ball would be constant during the descent. Thus, the SUVAT equations would apply.
Let
 denote the displacement of this stone during the fall. Let
denote the displacement of this stone during the fall. Let
 and
and
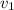 denote the velocity of this ball at the beginning at the end of the fall, respectively. Let
denote the velocity of this ball at the beginning at the end of the fall, respectively. Let
 denote the acceleration of this ball. The SUVAT equation
denote the acceleration of this ball. The SUVAT equation
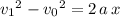 would apply.
would apply.
Rearrange the equation to find an expression for
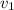 , the velocity of this ball at the end of the fall:
, the velocity of this ball at the end of the fall:
 .
.
If the final velocity of the ball is in the same direction as the displacement (downwards), then
 , such that
, such that
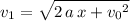 .
.
The acceleration of this ball during the fall should be equal to the gravitational field strength:
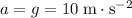 .
.
The displacement of the ball during the fall would be
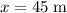 .
.
The question states that the ball was "dropped" from the given height. Thus, the initial velocity of the ball would be
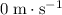 . (That is,
. (That is,
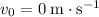 .)
.)
Substitute these values into the expression for
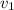 and evaluate:
and evaluate:
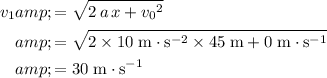 .
.
Therefore, the velocity of this ball right before landing would be
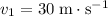 .
.