For the system of equations:

We can start by solving one of the equations for one of the variables and substituting into the other equation.
Since x has a quadratic term in the first equation, we can start by finding x first. To do this, we will need to substitute y and it is alredy solved in the first equation.
So, the first step is to substitute the first equation into the second:

Now, we have a quadratic equation, so we can apply the quadratic formula to find its zeros:
![\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}=\frac{-2\pm\sqrt[]{(-2)^2-4\cdot1\cdot(-8)}}{2\cdot1} \\ x=\frac{-2\pm\sqrt[]{4+32}}{2}=\frac{-2\pm\sqrt[]{36}}{2}=(-2\pm6)/(2)=-(2)/(2)\pm(6)/(2)=-1\pm3 \\ x_1=-1+3=2 \\ x_2=-1-3=-4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/hhe00xlxqm4catpi9gx93esptj4p12ru2w.png)
So, we have found two possible values for x.
Now, we need to find the corresponding values for y.
For x₁ = 2, we substitute it into either equations, let's do into the second:
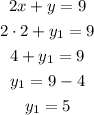
So, x₁ = 2 and y₁ = 5 is one of the solutions.
For x₂ = -4, we have:
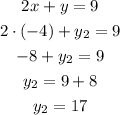
So, x₁ = -4 and y₁ = 17 is the second solution.
So, the solutions for this system of equations is (2, 5) and (-4, 17).