Question

If 4000 dollars is invested in a bank account at an interest rate of 5 per cent per year,Find the amount in the bank after 5 years if interest is compounded annually:Find the amount in the bank after 5 years if interest is compounded quarterly:Find the amount in the bank after 5 years if interest is compounded monthly:Finally, find the amount in the bank after 5 years if interest is compounded continuously:

Answer 1

The formula to calculate the amount of a value that is subject to a compounded interest is shown below:

`A=P\cdot(1+(r)/(n))^(nt)`

Where A is the final amount, P is the principal invested, r is the annual interest rate, n is the times it get compounded in a year and t is the elapsed time.

When we need to compound an amount quarterly, it will be compounded 4 times in a year, therefore n is equal to 4.

`\begin{gathered} A=2000\cdot(1+(0.07)/(4))^(4\cdot6) \\ A=2000\cdot(1+0.0175)^(24) \\ A=2000\cdot(1.0175)^(24) \\ A=2000\cdot1.5164=3032.8 \end{gathered}`

When we need to compound it monthly, it will be compounded 12 times in a year, therefore n is equal to 12.

`\begin{gathered} A=2000\cdot(1+(0.07)/(12))^(12\cdot6) \\ A=2000\cdot(1.00583)^(72) \\ A=2000\cdot1.51974=3039.48 \end{gathered}`

When we need to compound it continuously the formula will change to the one shown below:

`A=P\cdot e^(rt)`

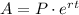
Applying the data we have:

`\begin{gathered} A=2000\cdot e^(0.07\cdot6) \\ A=2000\cdot e^(0.42) \\ A=2000\cdot1.52196 \\ A=3043.92 \end{gathered}`