We must solve for g the following equation:
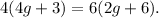
1) First, we apply the distributive property for the multiplication:
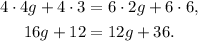
2) We pass the +12 on the left as -12 on the right:
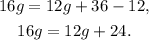
3) We pass the +12g on the right as -12g on the left:
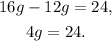
4) Finally, dividing both sides by 4, we get:
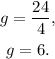
Answer
g = 6