The question (growth rate) deals with exponential functions. Growth occurs at a constant growth rate and is modeled by the standard equation:

We were given the following information from the question:
Initial or starting amount of bacteria cells, a = 800
Growth rate, r = 3.2% =3.2/100 = 0.032
Time, x = 35 hours
We will proceed to substitute these variables into the growth equation, we have:
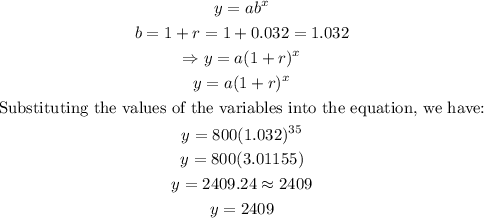
Therefore, after 35 hours, the number of bacteria cells would have increased from 800 to 2409
We will proceed to graph the growth function as shown below: