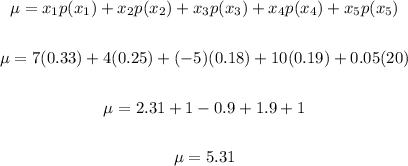Question

Your expected value calculations for your Friday night activities proved to be very accurate, so you wish to do the same thing for Saturday night. Your friends havedecided to go to dinner together. You decide that there are 5 possible outcomes. After each is the probability and relative pleasure rating of that outcome that youcalculated.Outcome 1: All of your good friends show up. Probability: 0.33. Relative pleasure rating: 7.Outcome 2: Your good friends, but also your one annoying friend shows up. Probability: 0.25. Relative pleasure rating: 4.Outcome 3: Only your one annoying friend shows up. Probability: 0.18. Relative pleasure rating: -5.Outcome 4: Your good friends, plus that one person you have a crush on show up. Probability of 0.19. Relative pleasure rating: 10Outcome 5: Only that one person that you have a crush on show up. Probability: 0.05. Relative pleasure rating: 20.Compute the expected value of your relative pleasure rating for going out to dinner with your friends. Select the correct value from the options below.5.3112.966.194.487.443.41

Answer 1

Answer:

5.31

Step-by-step explanation:

The expected value of a probability distribution is:

`\mu=\sum_^xp(x)`

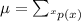
where x is the number of trials (or rating in this case)

p(x) is the probability of success

For outcome 1:

x = 7, p(x) = 0.33

For outcome 2:

x = 4, p(x) = 0.25

For outcome 3:

x = -5, p(x) = 0.18

For outcome 4:

x = 10, p(x) = 0.19

For outcome 5:

x = 0.05, p(x) = 20

Substituting these values in the expected value formula for probability distribution

`\begin{gathered} \mu=x_1p(x_1)+x_2p(x_2)+x_3p(x_3)+x_4p(x_4)+x_5p(x_5) \\ \\ \mu=7(0.33)+4(0.25)+(-5)(0.18)+10(0.19)+0.05(20) \\ \\ \mu=2.31+1-0.9+1.9+1 \\ \\ \mu=5.31 \end{gathered}`