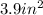Question

Find the area of the yellow region.Round to the nearest tenth.D6 in6 inArea = [? ] in^2

Answer 1

We have a square with two half circles drawn, and we need to find the area of the yellow region.

The procedure we will follow is: first calculate the area of the square, then subtract the area of the two half circles (which make up 1 circle) and then divide the result by 2.

Step 1. Find the area of the square.

The formula to find the area of a square is:

`A_{\text{square}}=l^2`

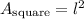
Where l is the length of the side of the square

`l=6in`

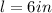
Thus, the area of the square is:

`\begin{gathered} A_{\text{square}}=(6in)^2 \\ A_{\text{square}}=36in^2 \end{gathered}`

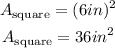
Step 2. Calculate the area of the two half circles.

Between the two half circles drawn, we can form one whole circle.

The formula to find the area of a circle is:

`A_{\text{circle}}=\pi r^2`

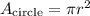
Where r is the radius of the circle and π=3.1416.

The radius of the circle of half of the side of the square:

`\begin{gathered} r=(6in)/(2) \\ r=3in \end{gathered}`

Thus, the area of the circle is:

`\begin{gathered} A_{\text{circle}}=(3.1416)(3in)^2 \\ A_{\text{circle}}=(3.1416)(9in^2) \\ A_{\text{circle}}=28.2744in^2 \end{gathered}`

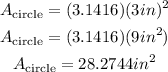
Step 3. The yellow area will be the result of subtracting the area of the circle to the area of the square and dividing the result by 2:

`A_{\text{yellow}}=\frac{A_{\text{square}}-A_{\text{circle}}}{2}`

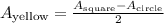
Substituting the known values:

`A_{\text{yellow}}=(36in^2-28.2744in^2)/(2)`

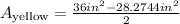
Solving the operations:

`\begin{gathered} A_{\text{yellow}}=(7.7256in^2)/(2) \\ A_{\text{yellow}}=3.863in^2 \end{gathered}`

Finally, we round the answer to the nearest tenth:

`A_{\text{yellow}}=3.9in^2`

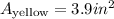
Answer:

`3.9in^2`